Home >> Fields, gravitational fields 1

Newton's Law of Gravitation

For two masses displaced a distance apart,
the gravitational force of attraction of one mass on the other is directly proportional to the product of the two masses and inversely proportional to the square of the distance between them.

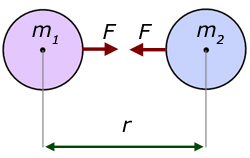
If the masses are m₁ and m₂ , with their centres of mass displaced a distance r apart, then the force of attraction F of one mass on the other is described as:

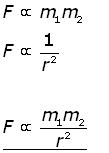
The proportionality can be made into an equation using a constant of proportionality. This constant we call G, the Universal Gravitational Constant.

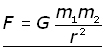
G = 6.67 x 10^-11 N m² kg^-2

Gravitational force is very weak! This can be shown by considering two 1 kg masses 1 m apart. The gravitational force between them is given by:

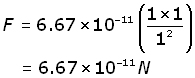
The gravitational force between everyday objects is so small as to be almost irrelevant.

back to top

Variation of 'g' with distance from the Earth's centre

To understand this work we must recall that 'g' is the acceleration due to gravity (9.8 ms ^-2). This value is for the surface of the Earth. Weight W is the force of attraction of the earth on a mass. For a mass m, the weight is given by:

The mathematical treatment depends on two assumptions:

1. The value of g is the same at a distance from a mass, whether the mass is in the shape of a spherical shell or concentrated in the centre.

2. The value of g everywhere inside a spherical shell is zero.

 

NB the spherical shell and central mass have uniform density

First consider a mass m on the surface of the Earth. The force of attraction between the mass and the earth is its weight W. This is also equal to the force F between the mass and the Earth, given by Newton's Law.

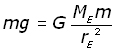
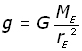                (i                   

Where M_E is the mass of the Earth, r_E its radius.

Now let us consider the value of g at a distance r from the Earth.

case where r > r_E

If this new value is g_r , then by similarity with equation (i,

                (ii                 

Dividing equation (ii by equation 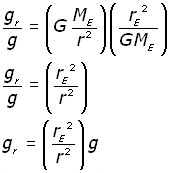(i,

(iii             

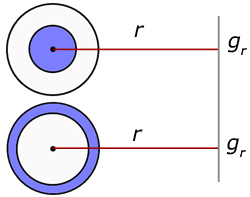
case where r < r_E

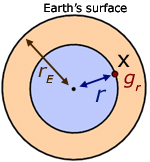
In the diagram the point X is inside the earth at a distance r from the centre.

From our initial assumptions, the value of g_r is a result of the gravity from a sphere of radius r .

If M_S is the mass of the sphere, then by comparison with equation (i ,

                 (iv                 

NB the effect of matter (in the form of a shell) above point X has no effect on the value of g_r

let us assume that masses have uniform density ρ (rho).

Remembering that m = ρV , the mass M_S of the internal sphere and the mass M_E of the Earth is given by:

dividing the first equation by the second,

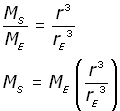
Substituting for M_S from equation (iv ,

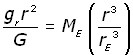
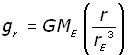
recalling that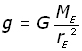

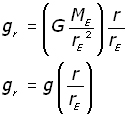
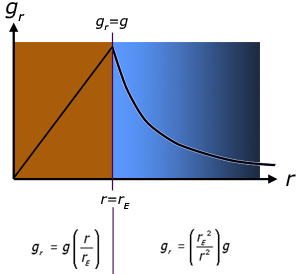
NB   g_r = g when r = r_E

Summary

So for inside the Earth, g_r is directly proportional to r . The graph is therefore a straight line through the origin.

For outside the Earth, g_r follows a function similar to y = x^-2 , where x decreases steadily, approaching zero at infinity.

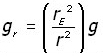
where r_E and g are constants

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]