Home >> Mechanics, statics, forces in equilibrium

In this work it is assumed that all the forces act in one plane. They are coplanar.

In this context the word equilibrium means that the coplanar forces are in balance and there is no net force acting.

Below is a list of methods for describing forces in equilibrium acting on a particle.

Vector Method

The condition for equilibrium of a particle:

the vector sum of forces(the resultant) is the null vector

This means that the multipliers for the i, j and k unit vectors are each zero.

Example #1

A particle at rest has forces (2i + 3j), (mi + 6j) and (-4i + nj) acting on it.

What are the values of m and n ?

For equilibrium, all the forces when added together(the vector sum) equal zero.

The scalar multipliers of each unit vector equal zero.

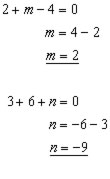
Ans.  m = 2  and  n = -9

Example #2

A particle at rest has an unknown force F and two other forces (2i - 5 j), (-3i + j), acting on it.

What is the magnitude of F ? (2 d.p.)
(all forces in Newtons, N)

for equilibrium the vector sum equals zero

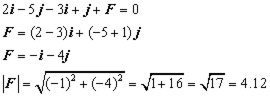
Ans. force F = 4.12 N

back to top

Resolution Method

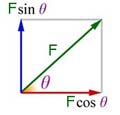
A force F can be replaced by two vectors that are at right angles to eachother, passing through the point of application. Hence if the angle between one component vector and the original vector is θ(theta), then the two components are Fsinθ and Fcosθ .

Problems are solved by resolving all the vectors into their horizontal and vertical components.

The components are then resolved vertically and then horizontally to obtain two equation. These can be solved as simultaneous equations.

Example

A 2 kg mass is suspended by two light inextensible strings inclined at 60 deg. and 45 deg. to the vertical.

What are the tensions in the strings?(to 2 d.p.)
(assume g=10 ms^-2 )

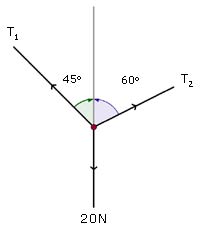
Ans. the tensions in the strings are 14.6 N and 17.9 N

back to top

Triangle of Forces

When 3 coplanar forces acting at a point are in equilibrium, they can be represented in magnitude and direction by the adjacent sides of a triangle taken in order.

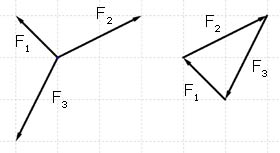
Example

Using the results from the previous example, the three forces acting on the 2 kg mass can be represented by a scale diagram.

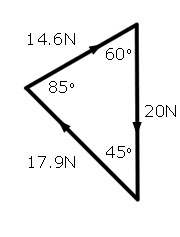
Our starting point is the 20N force acting downwards.

One force acts at 45 deg. to this line and the other at 60 deg.

So to find the magnitude of the two forces, draw lines at these angles at each end of the 20N force.

Where the lines cross gives a vertex of the triangle.

Measuring the lengths of the lines from this to the ends of the 20N force line will give the magnitudes of the required forces.

back to top

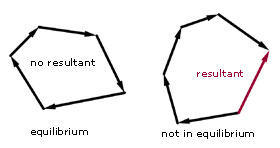
Polygon of Forces

For equilibrium, forces are represented in magnitude and direct to form a polygon shape.

If a number of forces are acting at a point, then the missing side in the polygon represents the resultant force.

Note: the arrow direction on this force is in the opposite direction to the rest.

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]