Home >> Quantum, photo-electric effect
photons |
History
Hertz discovered the photo-electric effect in 1887. His experiment concerned two parallel metal electrodes, with a p.d. across them. He observed that when ulta-violet light was shone on the electrodes an electric spark jumped between them. Many of the properties of the effect were established by Hallwachs and Lenard in the years leading up to Einstein's theory in 1905.
The Photon Model
Max Planck(1901) first proposed the idea that light was emitted as discrete packets of energy called quanta. He also showed that each packet (quantum) had energy given by the equation:
where,
E = energy (J)
h = Planck's constant, 6.626 x 10-34 Js
ν(nu) = frequency of light radiation (Hz, s-1)
However, Einstein, as part of his photo-electric effect theory, described these quanta as streams of particles, which he termed photons.
Observations
1. Emission of photo-electrons only occurs if the frequency of incident radiation exceeds a minimum value called the 'threshold frequency'.
2. The emission of photo-electrons starts immediately the surface becomes irradiated(provided the frequency of the radiation is above the thresh-hold frequency).
3. If the incident radiation has a frequency above the thresh-hold frequency:
( no. electrons emitted/sec. ) 
( radiation intensity )
4. Increasing the frequency of the incident radiation has the effect of increasing the kinetic energy of all emitted electrons. Hence the maximum kinetic energy an electron may have is increased by increasing frequency.
5. Radiation intensity is independent of electron kinetic energy. The kinetic energy of electrons is soley controlled by the radiation frequency.
Wave Theory predictions
Classical wave theory predicts that energy is carried in the wave-front. Electrons absorb the energy from the wave until the level exceeds the work function*. Electrons are then released from the surface of the metal.
*W (or Phi Φ) minimum energy to remove an electron
Three main predictions come from this classical explanation:
1. Radiation intensity is proportional to the resulting maximum electron kinetic energy.
(radiation intensity) (maximum electron kinetic energy)
2. The effect should occur for any frequency of light
3. There is a delay between the radiation contact with the surface and the first release of electrons.
Einstein's Photo-Electric Effect Theory
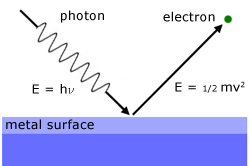
The theory is based on a beam of light being considered as a stream of photons, each with energy hν.
Before explaining the theory in more detail, it is important to appreciate what is meant by 'the intensity of light'.
Note there is no diminuition of photon energy, whatever the distance travelled.
Intensity (I) beam of light (no.photons/m2/sec.)
Einsein's big idea, in essence, was that when a photon collides with an electron there are two possible outcomes:
1. the photon reflects from the electron with no energy transfer
2. the photon is absorbed by the electron and gives up ALL its energy to it
Photons are paired with electrons. So there is no question of one photon sharing energy with more than one electron.
intensity of light ( no. electrons emitted by a surface)
or more accurately,
(no.photons/m2/sec.) ( no. electrons/m2/sec.)
So when a photon arrives at the surface, an electron is emitted. This exlains the instantaneous nature of the phenomenon.
The photon energy received is used to overcome the forces holding the electron within the surface and to give it kinetic energy to escape.
Einstein's photo-electric effect equation describes this process in more detail:
Note this involves the maximum electron kinetic energy. Many electrons emerge from the surface with less than the maximum energy. This is a result of energy lost in collisions before they are free.
W is called the 'work function' of the surface. It is a measure of the energy that binds each electron into the surface. The constant is different for different materials.
That there must be a minimum frequency for electron emission is implicit.
If
there is not enough energy available to release an electron.
However, that particular frequency for an electron to be released is given by:
where νo is the threshold frequency.
Using c=νoλo and substituting for νo = c/λo , the threshold wavelength λo is given by:
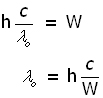
Millikan's apparatus - stopping potential
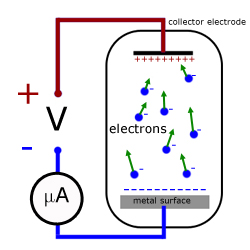
In 1916 Millikan devised a series of experiments that completely vindicated Einstein's theory. Using monochromatic light, the apparatus tested three surfaces in turn (lithium, sodium and potassium). He found that altering the potential between the surface and the electron collector electrode, altered the 'electron current'.
When a small positive potential was applied to the metal, only electrons with enough KE escaped to impact on the collector electrode. The remainder were pulled back to the surface. So only a small electric current was detected at the electrode.
With increased +ve potential, the electron current was reduced.
Eventually there came a point when the current reduced to zero. This corresponded to electrons with the maximum KE being stopped from reaching the collector. This p.d. between both electrodes is called the stopping potential V .
We can now integrate 'stopping potential' into the photo-electric effect equation.
The work done by an electron in moving against the 'stopping potential'(ie against the 'electric field' ) is equal to the maximum KE of the electron.
from Einstein's photo-electric effect equation:
substuting for KE,
rearranging into the form for a straight line ' y = mx + c '
For different materials, a plot of V against frequency ν(nu) is a straight line, with intercepts on the V-axis and the ν-axis.
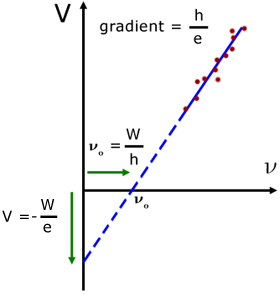
intercept on V-axis ( ν = 0 ) is: 
intercept on the ν-axis (V = 0 ) is: 
where νo is the threshold frequency
gradient is given by : 
notes
1. for different materials the graph has the same gradient but different intercepts
2. measurements of W (the work function) can be made
3. measurements of h (Planck's constant) can be made
this week's promoted video
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]