Home >> Waves, beats

Description

Beats is a phenomenon associated with sound waves, though the effect applies to all waves.
Essentially, when two similar frequencies ( f₁ , f₂) are sounded, a third much lower frequency is heard at the same time.
This third frequency is called the beat frequency ( f_B ).
The beat frequency is simply the difference between the two original frequencies.

The beat frequency is measured from the rise and fall in the loudness/volume.

There is yet another frequency, the combined frequency( f_C). This is the result of superposition of the two original frequencies. The combined frequency is simply the average of these frequencies.

Since the frequencies f₁ , f₂ are almost the same, the change in frequency to f_C is hardly noticeable.

An example of the effect is the sound from a twin engined prop. aircraft. There is a periodic 'wow' or 'drone' noise produced as a result of the change in r.p.m. from the different propeller blades.

Explanation

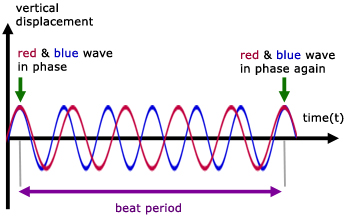
The effect is a result of superposition of two sound wave frequencies producing a succession of constructive and distructive interference.
When the two frequencies are in phase they add, producing a wave with double the amplitude.
When the two waves are out of phase, they destroy eachother.

back to top

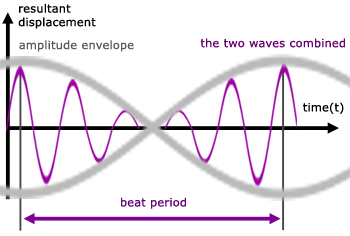
Theory

Consider our two original frequencies f₁ and f₂.

In time t the number of cycles completed by each frequency is f₁t and f₂t (no. cycles = no cyles per second x no. seconds).

Let us choose the time t such that the first wave completes one more cycle than the second.

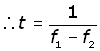
From the first of two images (above), t is the time interval between the waves being in phase with each other.

So t is the beat period T (time for one complete 'beat' wave).

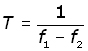
For any wave, period and frequency are inversely proportional to one another.

So for beat period T and beat frequency f_B ,

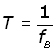
hence, by similarity between the last two equations,

assuming f₁ > f₂    

back to top

Measuring an unknown frequency

The method is to use a frequency( f_U ), where only an approximate value is known.
This is used with a known frequency( f_K ) close to the approximate value of f_U to produce beats.

The beat frequency ( f_B ) is given by:

or (depending on the relative magnitudes of f_K and f_U )

bringing the two equations together,

This is quite an accurate method, achieving results of 0.01% accuracy.

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]