Home >> Waves, waves in pipes
closed pipes |
Pipes produce standing waves similar to stretched strings. However it must be emphasized that in stretched strings the waves are transverse, while in pipes the waves are longitudinal.
Transverse - particles of the wave vibrate at right angles to the direction of travel of the wave.
Longitudinal - particles of the wave vibrate in the same line as the direction of travel.
Closed pipes
In the diagrams, P is the site of a node, while Q is at an antinode.
Nodes are always formed at the closed end of a pipe, where the air cannot move.
Antinodes are always formed at the open end of pipes.
As with stretched strings, the distance between node and antinode is 1/4 of a wavelength.
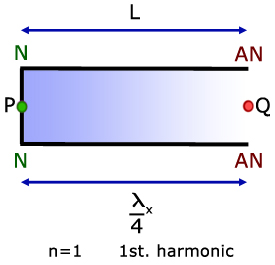
The diagram above represents the Fundamental Frequency, where n=1. This is the 1st harmonic.
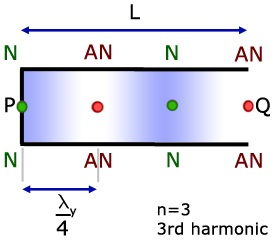
The diagram above represents the 3rd harmonic, sometimes called the First Overtone.
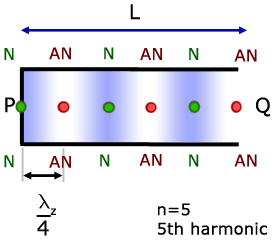
The diagram above represents the 5th harmonic, sometimes called the Second Overtone.
Looking at the different wavelengths in terms of the length of the pipe L ,
![]()
we can then make wavelength the subject of each equation.
![]()
Using the wave equation and making the frequency f the subject:
![]()
Substituting the different values of wavelength to obtain different expressions for frequency:
![]()
Looking at the form of these equations it is observed that each is a multiple of fx (the Fundamental Frequency).

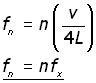
where n is 1, 3, 5, ... (odd)
Open pipes
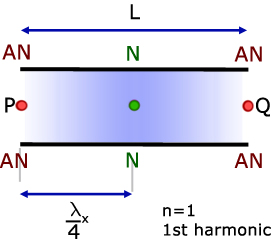
The diagram above represents the Fundamental Frequency, where n=1. This is the 1st harmonic.
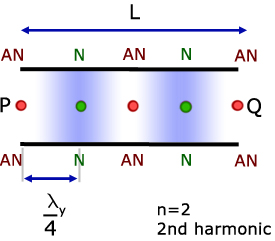
The diagram above represents the 2nd harmonic, sometimes called the First Overtone.
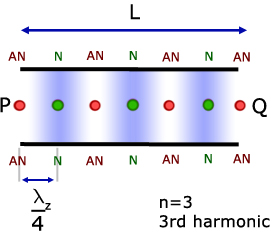
The diagram above represents the 3rd harmonic, sometimes called the Second Overtone.
Looking at the different wavelengths in terms of the length of the pipe L ,
![]()
We can then make wavelength the subject of each equation.
![]()
Using the wave equation and making the frequency f the subject:
![]()
We can now substitute the different values of wavelength to obtain different expressions for frequency:
![]()
Looking at the form of these equations it is observed that each is a multiple of fx (the Fundamental Frequency).

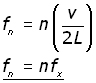
where n is 1, 2, 3, 4, 5, ... (odd + even)
A comparison of 'closed' and 'open' pipes
1. Comparing expressions for the Fundamental Frequency (n=1) for closed and open pipes respectively,
![]()
For a pipe of the same length L, the open pipe frequency is twice that of the closed pipe frequency.
![]()
2. For a given length of pipe, an open pipe gives more harmonics (odd & even) than a closed pipe (odd only). This results in a richer note from the open pipe.
End correction
The 'end correction' (c) is a length that must be added on to the the length (Lo) of a pipe to take account of antinodes extending beyond the open end of the pipe.
End correction for a closed pipe
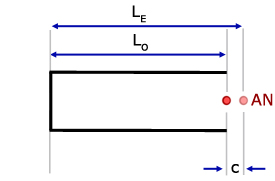
The effective length (LE) is given by:
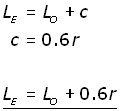
where r is the radius of the pipe
End correction for an open pipe
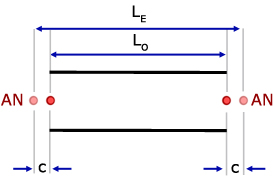
The effective length (LE) is given by:
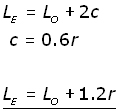
where r is the radius of the pipe
this week's promoted video
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]
