Home >> Mechanics, momentum & impulse, coefficient of restitution
coeffficient of restitution |
The Coefficient of Restitution
The Coefficient of Restitution (e) is a variable number with no units, with limits from zero to one.
0 ≤ e ≤ 1
'e' is a consequence of Newton's Experimental Law of Impact, which describes how the speed of separation of two impacting bodies compares with their speed of approach.
note: the speeds are relative speeds

If we consider the speed of individual masses before and after collision, we obtain another useful equation:
uA = initial speed of mass A
uB = initial speed of mass B
vA = final speed of mass A
vB = final speed of mass B
relative initial speed of mass A to mass B = uB - uA
relative final speed of mass A to mass B = vB - vA
![]()
note: in this equation the absolute of uB - uA and vB - vA are used ( |absolute| so there is no net negative result )
Example
A 5 kg mass moving at 6 ms-1 makes a head-on collision with a 4 kg mass travelling at 3 ms-1 .
Assuming that there are no external forces acting on the system, what are the velocities of the two masses after impact?
(assume coefficient of restitution e = 0.5 )
uA = initial speed of 5 kg mass (mass A)= 6 ms-1
uB = initial speed of 4 kg mass (mass B)= 3 ms-1
mA = 5 kg mB = 4 kg
vA = final speed of mass A vB = final speed of mass B
momentum before the collision equals momentum after
hence,
mA uA + mB uB = mA vA + mB vB
also
![]()
substituting for e, mA , uA , mB , uB we obtain two simultaneous equations from the conservation of momentum,
5 x 0.6 + 4(-3) = 5 vA + 4 vB
3 - 12 = 5 vA + 4 vB
-9 = 5 vA + 4 vB
5 vA + 4 vB = -9 (i
from the coefficient of restitution expression,
![]()
0.5(uA - uB) = vB - vA
(0.5 x 6) - (0.5(-3)) = vB - vA
3 + 1.5 = vB - vA
4.5 = vB - vA
vB - vA = 4.5 (ii
multiplying (ii by 5 and adding
5 vA + 4 vB = -9
- 5 vA + 5 vB = 22.5
9 vB = 13.5
vB = 1.5 ms-1
from (ii
1.5 - vA = 4.5
vA = 1.5 - 4.5 = -3
vA = -3 ms-1
Ans. The velocities of the 5 kg and 4 kg masses are -3 ms-1and 1.5 ms-1, respectively.
Oblique Collisions
For two masses colliding along a line, Newton's Experimental law is true for component speeds. That is, the law is applied twice: to each pair of component speeds acting in a particular direction.
Example
A particle of mass m impacts a smooth wall at 4u ms-1 at an angle of 30 deg. to the vertical.
The particle rebounds with a speed ku at 90 deg. to the original direction and in the same plane as the impact trajectory.
What is:
i) the value of the constant 'k' ?
ii) the coefficient of restitution between the wall and the particle?
iii) the magnitude of the impulse of the wall on the particle
i) There is no momentum change parallel to the wall.
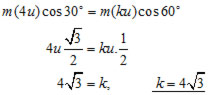
ii) The coefficient of restitution'e' is the ratio of the speed of separation to the speed of approach:
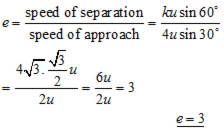
iii) The impulse is the change of momentum.
Since the vertical unit vectors are unchanged, the momentum change just concerns the horizontal vector components;
hence,
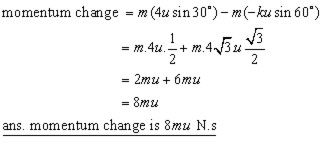
this week's promoted video
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]
