Home >> Waves, stationary waves

Introduction

Stationary or Standing waves have become very important in physics in the last hundred years or so. Understanding them has not only given insights into sound but many other important topics eg AC circuit theory, quantum mechanics, nanotechnology.

Formation of stationary waves

The conditions for standing waves are:

1. two waves travelling in opposite directions along the same line of travel and in the same plane

2. the waves have the same speed

3. the waves have the same frequency

4. the waves have the same approximate amplitude

As a result of superposition (waves adding/subtracting), a resultant wave is produced. Now, depending on the phase difference between the waves, this resultant wave appears to move slowly to the right or to the left or disappear completely. It is only when the phase difference is exactly zero, that is when the two waves are exactly in phase, that 'standing/stationary waves' occur.

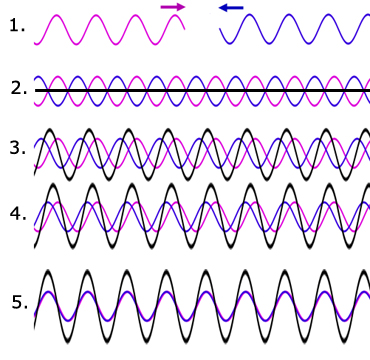
1. Two waves having the same amplitudes approach eachother from opposite directions.

2. The two waves are 180^o out of phase with eachother and therefore cancel out(black horizontal line).

3. The phase difference between the two waves narrows. The resultant grows but is not in phase with either of the two waves.

4. The phase difference between the two waves is narrower still. The resultant is larger but is still out of phase with the two waves.

5. The phase difference between the two waves is now zero. The resultant has its maximum value and is in phase with the two waves.

These 'in phase' waves produce an amplitude that is the sum of the individual amplitudes, the region being called an antinode. Between two antinodes is a region where the superposition is zero. This is called a node.

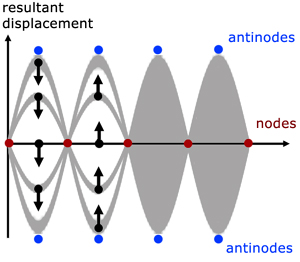
When the phenomenon is demonstrated with a horizontal vibrating string, the antinode areas appear blurred. To observe the motion of the string moving up and down a strobe lamp is used.

back to top

Properties of stationary waves

The diagram shows how a standing wave moves up and down over time.

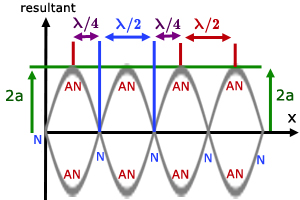
1. separation of adjacent nodes is half a wavelength (λ/2)

2. separation of adjacent antinodes is also λ/2

3. hence separation of adjacent nodes and antinodes is λ/4

3. the maximum amplitude is 2a (twice that of a single wave)

4. a standing wave does not transfer energy(its two components however, do transfer energy in their respective directions)

back to top

Stationary wave theory

Consider two waves, R and L, travelling in opposite directions. Their displacements y_R and y_L are given by*:

where,

*A derivation of the form of this equation will be provided under 'Derivations - for a deeper understanding' on the Waves menu at some future date.

When the two waves are superposed, the resultant displacement y_T is given by:

From double angle trigonometry, using one of the 'Factor Formulae' :

Comparing this with the expression for y_T , it is apparent that C= 2πft and D= kx .

Therefore,

If we now make,

Then y_T can be rewritten in a form similar to that of a simple sine wave y=asin(2πf)

The term A takes on the significance of being the vertical displacement of the standing wave. From the expression for A it can be seen that the magnitude of A depends on the lateral position x.

Consider the magnitude of A at different horizontal displacements (x) along the standing wave.

A = 0 at a node,    A = ± 2a at an antinode

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]