Home >> Quantum, quantum theory
summary |
|||
Quantum Theory summary
Quantum theory is used to explain interactions between matter and energy on the extremely small scale of atoms and sub-atomic particles.
basic points:
- energy comes in small, discrete units called photons
- elementary particles behave both like particles and like waves
- particle motion is random.
- uncertainty: particle position and momentum cannot be known at the same time
Planck's Quanta
Max Planck(1901) first proposed the idea that light was emitted as discrete packets of energy called quanta. He also showed that each packet (quantum) had energy given by the equation:
![]()
where,
E = energy (J)
h = Planck's constant, 6.626 x 10-34 Js
ν(nu) = frequency of light radiation (Hz, s-1)
However, Einstein, as part of his photo-electric effect theory, described these quanta as streams of particles, which he termed photons.
Wave-particle duality
It is a common mistake to think of particles as 'matter waves' or 'energy waves'(like photons).
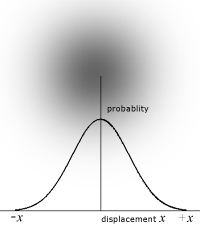
The wave properties of particles relates to their statistical position about a point. Rather than being like a billiard ball, a particle can be considered to be a fuzzy ball, where the depth of colour corresponds to position. So the particle spends most time at the centre of the fuzziness and least time at the edges.
Regarding the reality of particle duality, the Copenhagen interpretation is meant as clarification on the issue.
Essentially, the statement reads,
nothing is real unless it is observed. So a point of matter can be considered as a wave or a particle. If it behaves like a particle then it is a particle. If it behaves like a wave, then it is a wave.
...more on this in the section 'wave-particle duality'
Heisenburg's Uncertainty Principle
For a particle, position and momentum cannot be known at the same time.
Mathematically the product of the uncertainty in the position of a particle (Δx)and the uncertainty in the momentum (Δp) could never be less than a particular value. That particular value is related to Planck's constant h.
![]()
where 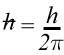
The Wave Function
The wave nature of matter is described in some detail by the Schrödinger Wave Equation. This is used to predict the future behavior of a dynamic system. Note, the waves referred to in the equation are 'probability waves'.
This is the Schrödinger wave equation for a free particle in one direction. The symbol Ψ is called the wave function.
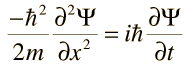
The wave function is used to give information on:
- probability distributions in 1D, 2D or 3D
- quantum states
- energy levels
There are other versions of the wave equation to cover different situations.
One version of the equation predicts where electrons exist around an atomic nucleus. Electrons are found in discrete 3D regions called 'orbitals'. Much of this work was done by Wolfgang Ernst Pauli in his famous 'exclusion principle'.
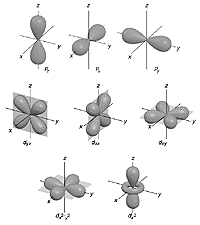
image courtesy of Chemistry Dept. University of Florida
Other wave solutions refer to individual particles, groups (beams) of particles, atoms and molecules.
Quantum Tunneling
This is a phenomenon relating to the probability wave of an electron and its range over an insurmountable barrier.
In classical terms, the electron does not have enough kinetic energy to jump a potential energy barrier. Compare a bouncing ball not able to bounce over a brick wall, which is too high.
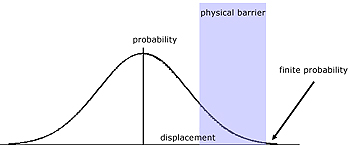
Electrons are particles of matter that exhibit a wavelike quality. According to quantum mechanical theory the wave function (probability wave) of the electron extends across the barrier.
So there is a finite possibility of it existing there.
Quantum tunneling is used in tunneling diodes and quantum tunneling composites(QTC's).
Tunneling diodes are important elements in high frequency devices like CRO's, frequency generators and detectors.
Quantum tunneling composites is the name given to the technology of 'touch screens'. These have applications in phones, TV's, cameras and monitors.
Quantum Entanglement
Quantumly entangled particles retain a connection between them even if separated across vast distances. So if one particle is disturbed, the other is also disturbed.
Einstein is said to have described the phenomenon as “spooky action at a distance” (a measure of his disbelief on the subject).
As an example, consider two electrons that through an interaction become entangled.
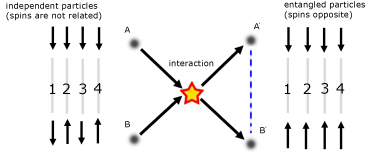
Each number in the diagram represents a run of the experiment, when the spins of particles A and B are measured.
The result of the entanglement is that spin states of the two particles become complementary. One state will be 'up' while the other is 'down'.
The shared state means that a change to one electron is reflected in the other. This has immense potential for the development of 'quantum computers' - computers that will be much faster than those at present.
Bose-Einstein Condensate (BEC)
At temperatures approach absolute zero, the atoms in a gas are in their lowest energy level. At these temperatures quantum mechanical effects become more apparent.
As a result of their probability positioning, atoms can be thought of as fuzzy balls. When the temperature decreases, the balls spread out and become less defined. Eventually a point is reached when their fuzziness(where they are positioned) overlaps.
At this time atoms lose their individual identities. They all have the same quantum state and coalesce into a single 'super atom'.
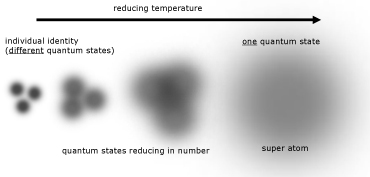
The properties of condensates are quite bizarre. These include:
- increased optical density(enough to slow photons down to walking speed!)
- super fluidity(absence of viscosity)
this week's promoted video
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]
