definitions
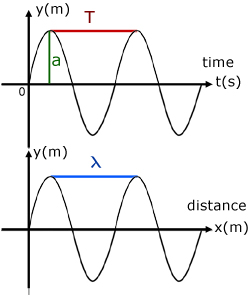
Wavelength ( λ ) is the horizontal distance along a wave between similar particles of the wave.
Displacement is the distance of a particle of the wave from its equilibrium position at any particular time
Amplitude ( a ) is the maximum displacement of a particle of the wave from its equilibrium position.
Period ( T ) is the time for one complete oscillation of the wave.
Frequency ( f ) is the number of waves produced per second.
Velocity ( v ) the velocity of a particle of a wave in the direction the wave is travelling.
Units |
||
wavelength |
metre |
m |
displacement |
metre |
m |
period |
second |
s |
frequency |
Hertz (Hz) |
s-1 |
velocity |
metres per second |
ms-1 |
Equations
The velocity ( v ) of a wave is expressed in terms of its frequency ( f ) and wavelength ( λ ):
The period and frequency of a wave are the inverse of each other:
Superposition
Superposition is when two waves are superimposed on eachother and add up. The phenomenon is described by the Principle of Superposition, which states:
When two waves are travelling in the same direction and speed, at any point on the combined wave the total displacement of any particle equals the vector sum of displacements of the waves.
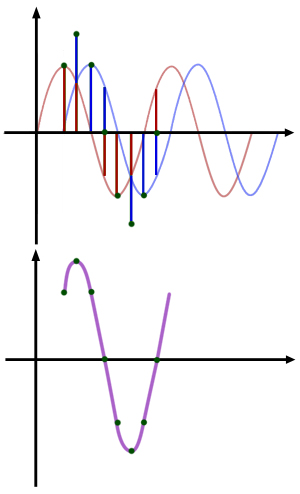
Look carefully at the diagram. The blue and red displacements add up algebraically.
Above the line is positive. Below the line is negative.
Hence a red displacement, above the line, on top of a blue displacement (of equal magnitude) below the line, will cancel out. This produces a point on the horizontal axis.
A red displacement, above the line, on top of a blue displacement, also above the line, will produce a displacement above the line equal to their sum.
A red displacement, below the line, below a blue displacement, also below the line, will produce a displacement below the line equal to their sum.
phase difference
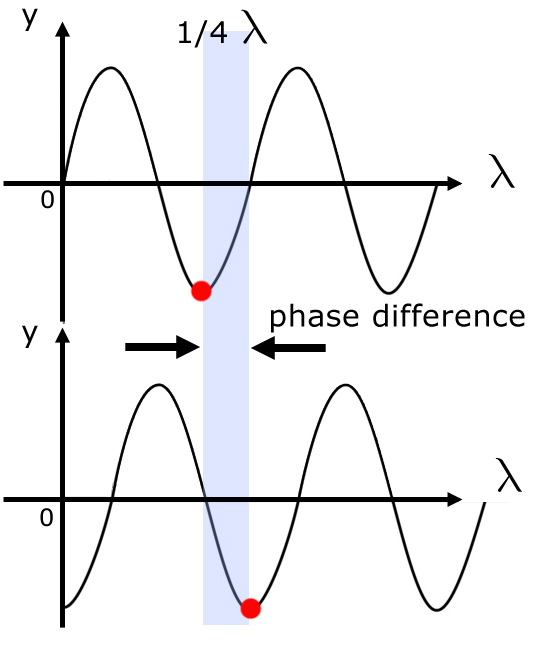
The phase difference of two waves is the horizontal distance a similar part of one wave leads or lags the other wave.
Phase difference is measured in fractions of a wavelength, degrees or radians.
In the diagram (above), the phase difference is ¼ λ.
This translates to 90o ( ¼ of 360o ) or π/2 ( ¼ of 2π ).
equation of a sinusoidal wave
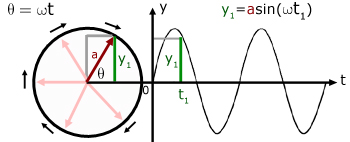
The graph represents a sinusoidal wave with displacement y at time t, vibrating at a frequency f and amplitude a. The motion can be described by the equation:
We can understand how this equation is constructed by introducing ω (omega) , the angular velocity (units rad s-1 ).
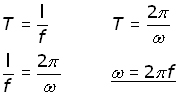
Substituting for 2πf, our equation then becomes,
The diagram shows how the value of the function (y) is calculated from the radius (a - red) of the circle sweeping out an angle θ (theta).
angle swept out = angular velocity x time of sweep
θ = ωt
From simple trigonometry, the value of y1 (green) is equal to asinθ.
The angle swept out at time t1 is ωt1 where ω is the angular velocity. This is a measure of the rotation of the a-vector in radians per second.
So the value y1 at time t1 is given by:
