Home >> Optics, microscopes

Magnifying Glass/Simple Microscope (image at Near Point)

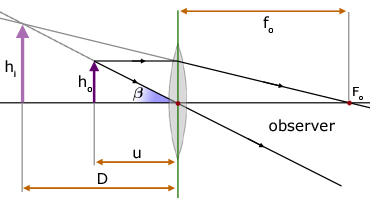
D is the Near Point of the eye. This is the closest an object can be to the eye and remain in focus.

By definition, magnification M is the height of the image h_i divided by the height of the object h_o :

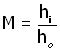
From the diagram, the angle β (beta) is given by:

rearranging,

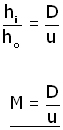
If we now use the lens equation:

In this case, v = - D . The image is virtual. So the sign is negative.

Hence,

Multipling both sides by D, and taking the second term over to the right,

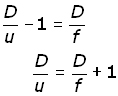
From our derivation of magnification M (above),

therefore our equation becomes,

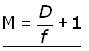
With the image at the near point, the magnification of an object by a magnifying glass can be simplified as:

where f is measured in centimetres(cm)

back to top

Compound microscope

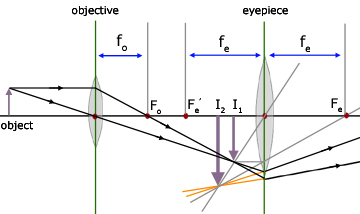
A microscope is very similar in arrangement to a telescope, the difference being in the focal length of the objective lens.
Microscope lens focal lengths are measured in mm, while telescope focal lengths can be measured in metres.
Essentially a real image is formed by the objective and this in turn is magnified by the eyepiece to form a virtual, erect image.
The first image (I₁) is positioned infront of the eyepiece, between f and the lens. The eyepiece produces the virtual image (I₂) behind the first image.
For the second image to be in focus, the distance between it and the eye must be at least 25 cm (D).

The magnifying power of a microscope is the product of the eyepiece and objective lens magnification.

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]